Diese Seite funktioniert nur mit Javascript.
Kontraktkurve und Kern5.1.1.2 Nutzenmöglichkeitskurve im PunktsinnMathematische Herleitung der Kontraktkurve
um Abschluss dieses Abschnitts stehen noch zwei kurze Punkte an: Erstens eine alternative grafische Darstellung der Kontraktkurve und zweitens der Einbezug weiterer Personen.
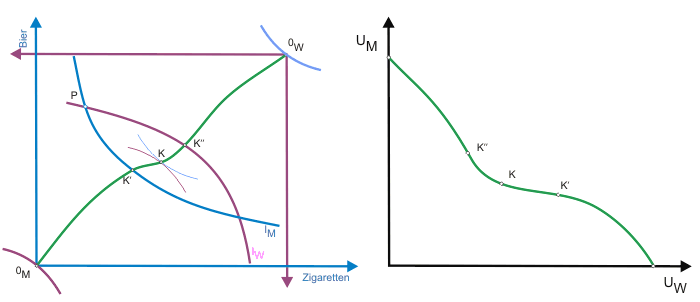
Für das erste Problem wird in Abbildung 1 ein sogenannter Nutzenraum aufgespannt. An den Achsen werden Maßzahlen für die Nutzen der beiden Konsumenten abgetragen (Nutzenindexwerte). Es handelt sich jedoch nach wie vor um ordinale Nutzenfunktionen. Der Konsument erreicht seinen höchsten Nutzen (höchste Indifferenzkurve), wenn er den gesamten verfügbaren Bier- und Zigarettenbestand erhält, also auf die Indifferenzkurve gelangt, die durch den Ursprung der Konsumentin in der Edgeworth-Box verläuft (s. 0W in Abbildung 1).
Im eigenen Ursprung 0M normieren wir den Nutzen des Konsumenten auf Null, da ihm hier keine Güter mehr verbleiben. Übertragen wir also die Nutzenniveaus jeden Punktes der Kontraktkurve in den Nutzenraum, erhalten wir einen stetig (monoton) fallenden Kurvenverlauf, dessen exakte Gestalt jedoch unbestimmt bleibt, da monotone positive Transformationen der Nutzenfunktion (stellen Sie sich die Achsen der Abbildung als Gummibänder vor) ohne Auswirkungen bleiben. Während wir auf der Kontraktkurve immer weiter nach unten wandern, nimmt der Nutzen der Konsumentin stetig zu, bis sie schließlich im Punkt 0M über die gesamte Güterausstattung verfügt und somit den größtmöglichen Nutzen erreicht.
Diese Kurve wird als Nutzenmöglichkeitskurve bei gegebener Güterausstattung oder als Nutzenmöglichkeitskurve im Punktsinn bezeichnet ("utility possibility curve in the point sense").
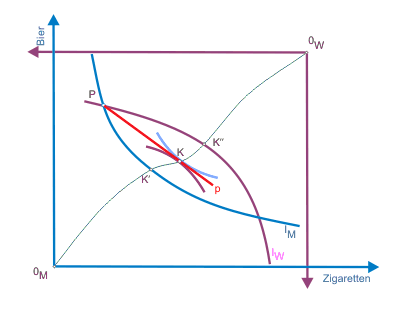
Für das zweite Problem sei angenommen, es gäbe eine Vielzahl (n) an Konsumenten, von denen keiner über hinreichende Macht verfüge, durch monopsonistisches Verhalten Preise zu beeinflussen. Dann gibt es auch Märkte für Bier und Zigaretten, auf denen sich die Preisbildung vollzieht. Mit gegebenen Preisen für Bier und Zigaretten ist aber auch das relative Preisverhältnis von Bier und Zigaretten, der Bierpreis in Zigarettenwährung, bekannt. Dieses Preisverhältnis ist in Abbildung 2 als Gerade p eingetragen. Konsequenterweise - das Tauschverhältnis ist ja nun bestimmt - ergibt sich für den Tauschprozess nun eine eindeutige Lösung auf dem Kern. Doch Vorsicht: das Preisverhältnis wird nur zufällig mit der Grenzrate der Substitution übereinstimmen, die dort gilt, wo die Preisgerade den Kern schneidet (s. Abbildung 2). Ist dies nicht der Fall, so ist die Lösung für keinen der beiden Tauschpartner optimal. Sie suchen sich andere unter den n-2 möglichen Tauschpartnern, die ihnen einen aus ihrer Sicht besseren Tausch anbieten. Die grafische Darstellung mit der Edgeworth-Box ergibt nun nicht mehr allzuviel her. Für diesen Punkt eignet sich besser die gewöhnliche Darstellung des Indifferenzkurvenschemas für eine Person. Dort ist in die Steigung der Budgetgeraden sozusagen eine "Tauschkurve" der n-1 möglichen Tauschpartner, die diese nicht preisgeben (gegebene Marktpreise bei Konkurrenz) und auf der das betrachtete Individuum seinen eigenen optimalen Punkt auswählen kann. Diese Überlegung kann man folgendermaßen einsehen: Der einzelne kann herrschende Preise nicht beeinflussen. Er weiß, dass es ihm nicht gelingen kann, ein Gut teurer als zu geltenden Marktpreisen zu verkaufen, da sich potenziellen Tauschpartnern sofort unzählige günstigere Angebote einholen könnten. Der Gesamtheit aller anderen Gesellschaftsmitglieder ist es nun gleichgültig, welchen Punkt auf der Tauschkurve das betrachtete Individuum auswählt, da die Tauschmöglichkeiten aller anderen davon nicht beeinflusst werden. Der Gesellschaft ist es einerlei, welchen Punkt ein einzelnes Wirtschaftsubjekt auf seiner Budgetgerade wählt.